Prism 3 -- User-Defined Equations

Step-by-Step Examples:
User-Defined Equations in Prism 3

Among the Classic equations and the Prism equation library are most of the curve-fit models that a biologist needs. Yet occasionally you may want to customize. For example, you may (a) need an equation of a form not built into Prism, (b) need to modify an existing equation, e.g., changing the two-site binding model to accommodate three sites, or (c) simply wish to rename the parameters in a built-in equation so that the curve-fit results will be labeled more appropriately.

In this example, we'll enter and fit data to a "user-defined" equation of a form not preprogrammed into Prism. The time course of total systemic absorption of a drug, expressed as the fraction (F) of the amount administered at a subcutaneous depot at time 0, is given by¹

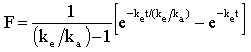
where t = time (min), and k_e and k_a are the first-order elimination and absorption rate constants (min-1), respectively. We'll plot an example time course and fit the curve to the data to obtain an estimate of the rate constants.

---

Enter the Data
In the Welcome to Prism dialog box, select Create a new project and Work independently. Under the X Column category, select Numbers, and under the Y Columns category, choose A single column of values. Enter the data as shown below.

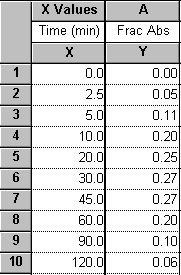
For this example, we're assuming that the Y values do not require correction by subtraction of a baseline-the minimum Y value is already 0. If you wish to subtract a baseline value from each Y value in a data set, read about automatic baseline corrections using Prism in the GraphPad Quick Answers Database.

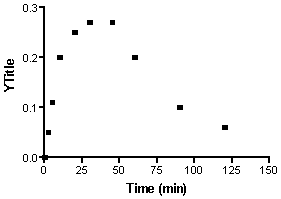
Click the yellow Graphs tab on the toolbar to view the graph:

---

Fit the Curve
With the graph displayed, click on the Analyze button. From the Curves & Regression category, select Nonlinear regression (curve fit).

In the Parameters: Nonlinear regression dialog box, choose More equations and, from the list below, click Enter your own equation.

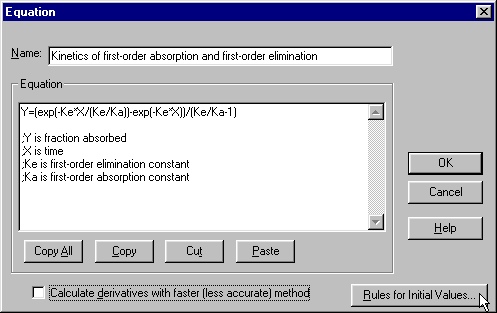
The Equation dialog is displayed. Enter a Name for this curve-fit analysis (which will be added to the "More equations" menu the next time you view it). Now enter your equation, in single-line form, into the Equation box. You are limited to certain types of equations and must adhere to a few simple syntax rules. 

Thus, you must designate the dependent and independent variables as Y and X, respectively, and you must write the equation so that Y is isolated on the left-hand side. Read the rules for entering user-defined equations in Prism, including the functions, or operators, that you may use. Our equation can be written on a single line as follows:

You can enter comments, to prompt your memory or to help other users understand your equation, by writing lines beginning with a semicolon.

When you're done entering your equation, click Rules for Initial Values.... Prism reads your equation and, after eliminating X, Y, and operators, arrives at the "parameters" to be fit, in this case, ke and ka. Curve fitting is an iterative, trial-and-error process of substituting values for the parameters in your equation in order to maximize the goodness of fit between your experimental data and the resulting substituted equation. Prism therefore must have an initial "guess" for the value of each parameter, that is, it must have a starting point for the process. When you use one of the Classic equations, Prism derives its own initial values, choosing numbers that are related to your experimental data by programmed "rules". For User-defined equations, Prism has no such rules, so you must provide either those rules or explicit initial values.

In the Rules for Initial Values dialog box, an explanatory note prompts you to enter a number into the first column and the relational rule, or "multiplier" into the second column.

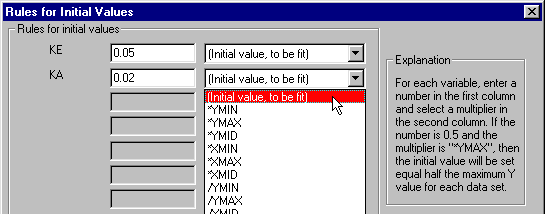
Your choices for the multiplier are of three kinds:

Initial value, to be fit

This choice indicates that the value in the first column is to be used explicitly. Select this option when there is no rule in the second column that reasonably allows derivation of the initial value from your experimental data. The drawback of this choice is that you may have to provide a new initial value each time you run this analysis. For this step-by-step example, we will select this option, since no reasonable rule is available.

The initial value estimate generally does not have to be very close to the actual fitted value, particularly when the equation has few parameters to be fit and your data doesn't have too much scatter.

The initial values that you enter might come from (a) your past experience or the experience of other investigators, including published values, (b) alternative methods of computation, or (c) a trial process, whereby you allow Prism to generate a curve using the values you supply and check to see if the result is reasonable. We'll illustrate the latter process below.

Don't forget to avoid entering "illegal" initial values. In our example, the equation is undefined for ke = 0, K_a = 0, and k_e = k_a.

A rule

If you can find a rule on this list that allows Prism consistently to derive an initial value from your data (i.e., if the rule holds as your data varies within reason from experiment to experiment), this is the best choice. You won't have to enter a new initial value each time you run the curve-fit analysis.

Constant value

This is one way to "fix", or hold constant, a curve-fit parameter. Prism will substitute the constant value provided in the first column as if you had written the value directly into your equation, and it will fit only the remaining parameters.

Too return to our example, suppose that we have entered the following initial values,

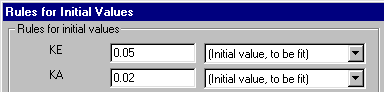
but before doing the curve fit, we would like to see how close a curve generated using those values will come to our data. We can do that by temporarily "fixing" all initial values. Click OK twice to return to the Parameters: Nonlinear regression dialog box, then click the Initial values... button. Check the box to Fix all variables to their initial values.

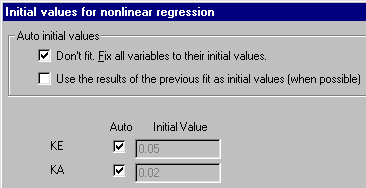
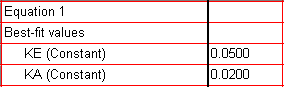
With all parameters fixed, Prism has nothing to "fit", and it will simply generate the curve for the equation with all of the fixed values substituted. Click OK twice to back through the dialog boxes and generate the curve. The Results sheet reports the "fixed" values for k_e and k_a.

Click the yellow Graphs tab to view the graph (the notations shown below were added manually using the text and drawing tools).

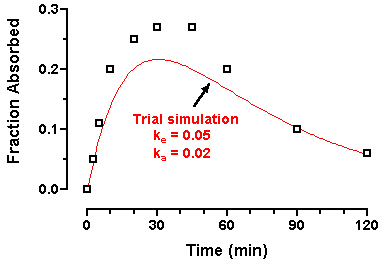
Since the curve is reasonably close to the points, we can now "unfix" the parameter values and allow Prism to fit the curve. Click the yellow Results tab and then the Change Params. button on the toolbar to return to the Parameters dialog. Click Initial values... and reset the checkboxes as shown here:

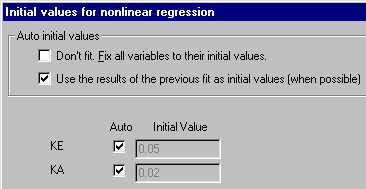
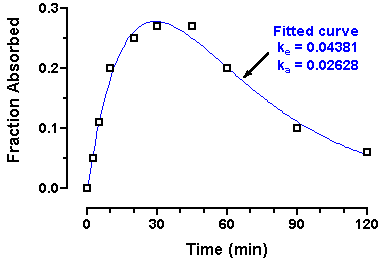
Click OK twice to back through the dialog boxes and fit the curve. The Results sheet appears, this time showing the fitted values for k_e and k_a.

Click the yellow Graphs tab to view the graph.

Two final notes:

1. Generating a trial curve based upon "fixed" parameters is not mandatory. If you are confident of your initial value settings, simply click OK three times from the Rules for Initial Values dialog to run the curve fit.

2. Ordinarily, the initial values need only be rough approximations of the fitted values, and it will not help to "fine-tune" them. But if the initial values produce a trial curve very far away from the data, Prism may not be able to figure out how to adjust the parameters for the next iteration, and it may abort the process.

---

1 Neubig, R. R., The Time Course of Drug Action, in Principles of Drug Action (W.B. Pratt and P. Taylor, eds.), 3rd Edition, Churchill Livingtone Inc., 1990.